题目信息

题目地址：https://leetcode-cn.com/problems/validate-binary-search-tree/

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

  • 节点的左子树只包含小于当前节点的数。
  • 节点的右子树只包含大于当前节点的数。
  • 所有左子树和右子树自身必须也是二叉搜索树。

示例 1:

1
2
3
4
5
输入:
    2
   / \
  1   3
输出: true

示例 2:

1
2
3
4
5
6
7
8
9
输入:
    5
   / \
  1   4
     / \
    3   6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
     根节点的值为 5 ，但是其右子节点值为 4 。

解法一：递归

和上题一样可以很好的想到递归的思路，左边都是越来越小，右边是越来越大。这个地方容易产生一种错觉。
1
错误思路及代码：
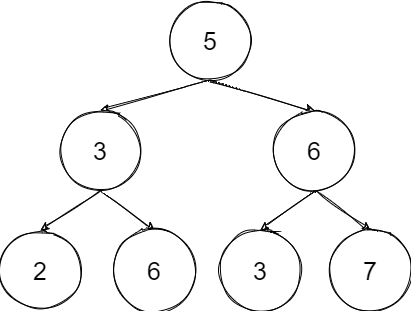
就是只比较左右子节点的与父节点大小关系，如上图第一次是满足的，接下来递归左节点但他没有子节点结束并返回true,递归右节点也满足关系，继续递归其右节点因无子节点结束，左边同理。整个递归完成最终是true,但因为3比根节点5小应该在左子树不满足二叉搜索树

1
2
3
4
5
6
7
8
public boolean isValidBST(TreeNode root) {
    if(root == null) return true;
    if(root.left != null && root.left.val >= root.val)
        return false;
    if(root.right != null && root.right.val <= root.val)
        return false;
    return isValidBST(root.left) && isValidBST(root.right);
}

那么问题就在于我们要比较的东西是什么？
2
对于叶子节点2来说它比3小就可以没有限制，对于叶子节点6的位置它只能大于3并且小于5才有效
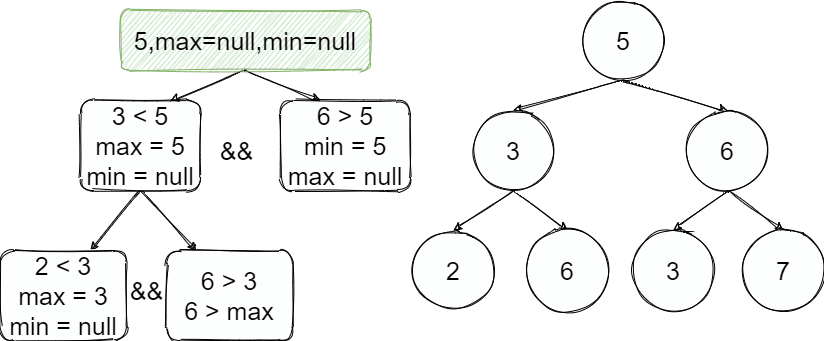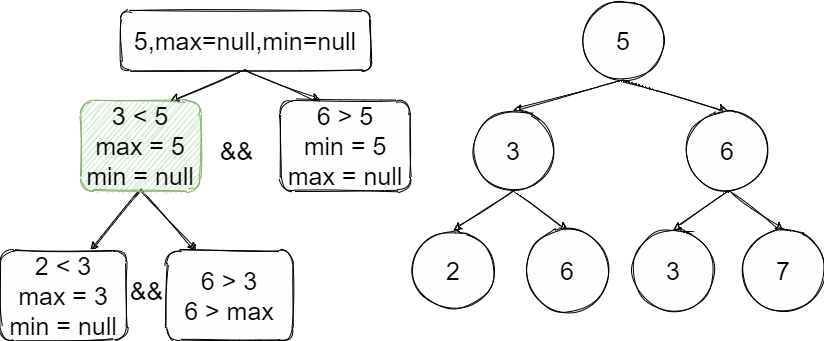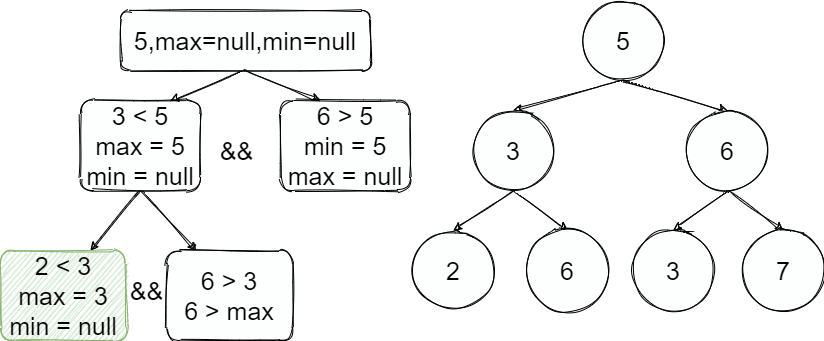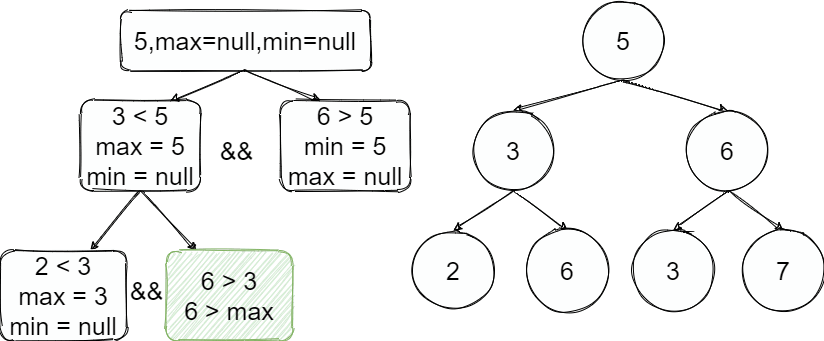
也就是说我们往左边走即是小那么就有一个上限之后不能超过，往右边走即是大就有一个下限。
3
按照整个过程如上图，从根节点开始往左进入递归，往左了以后这边的值都小于上限5并且3满足小于5继续递归找到2也是满足并且2之后的树上限是3，继续递归为空了出去，执行下一步的兄弟节点判断时超过了上线结束

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
public boolean isValidBST(TreeNode root) {
    return process(root, null, null);
}
//递归方法
public boolean process(TreeNode node, Integer min, Integer max) {
    if (node == null) return true;
    if (min != null && node.val <= min) return false;
    if (max != null && node.val >= max) return false;
    if (!process(node.right, node.val, max)) return false;
    if (!process(node.left, min, node.val)) return false;
    return true;
}

4

解法二：中序遍历

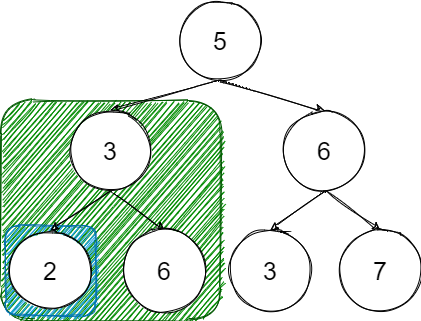
中序遍历是树的一种遍历方式，先数左子树在数中间在数右子树，那么通过中序遍历如果是真的二叉搜索树是一个从小打大的序列
5
上图中序遍历：[2,3,6,5,3,6,7]

1
2
3
4
5
6
7
8
9
10
11
12
//记录前一个
Integer pre = null;
public boolean isValidBST(TreeNode root) {
    if (root == null) return true;
    // 访问左子树
    if (!isValidBST(root.left)) return false;
    // 访问当前节点：如果当前节点小于等于中序遍历的前一个节点.即不满足
    if (pre != null && root.val <= pre) return false;
    pre = root.val;
    // 访问右子树
    return isValidBST(root.right);
}

6

总结

其实两种解法也都是属于深度优先，一个在过程中处理遍历方式为后序，一个是中序。使用不同的遍历过程那么就需要想清楚在这种遍历下处理判断逻辑。