题目信息

题目地址：https://leetcode-cn.com/problems/symmetric-tree/

给定一个二叉树，检查它是否是镜像对称的。

**示例1：**是对称的

1
2
3
4
5
    1
   / \
  2   2
 / \ / \
3  4 4  3

**示例2：**不对称

1
2
3
4
5
  1
 / \
2   2
 \   \
 3    3

解法一：递归

我们先来划分子问题，一个树对称也就最终根节点的左子树与右子树是对称的镜像的，那么要求左子节点与右子节点相等的同时左节点的左子树（右子树）与右节点的右子树（左子树）对称，还是画个图吧

我们传入这两颗树看是否对称，那么有三个操作：

  • 第一两个根节点是否相等
  • 第二它左子树是否与另外一个的右子树对称
  • 第三它的右子树是否与另外一个的左子树对称

每次递归传递一对树，直到最后叶子只有节点节点比较

1
2
3
4
5
6
7
8
9
10
11
12
public boolean isSymmetric(TreeNode root) {
    //第一次传root让下面顺便进行空判断
    return check(root, root);
}
public boolean check(TreeNode p, TreeNode q) {
    //都为空则没有子树，两个根相等就是对称
    if (p == null && q == null) return true;
    //不满足上面条件，则是一个有子树一个没有那么不对称
    if (p == null || q == null) return false;
    //三个条件结合
    return p.val == q.val && check(p.left, q.right) && check(p.right, q.left);
}

遍历了整颗树时间复杂度为O（n）,递归系统栈占用大小取决于树的层度这里不是完全二叉树所以它只是小于n空间复杂度为O（n）

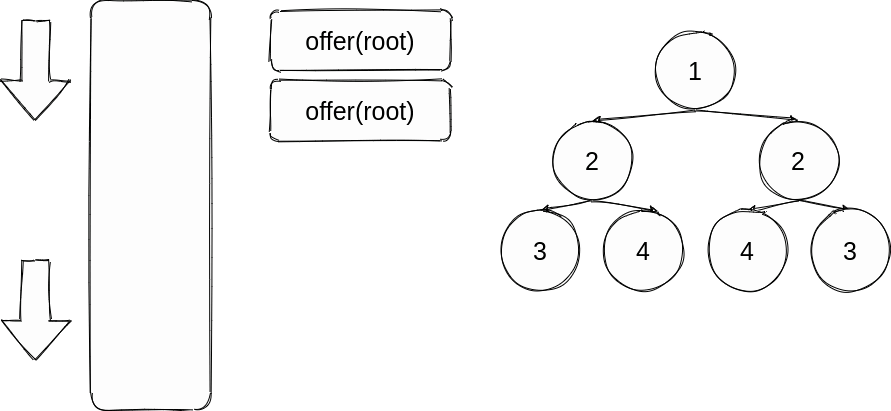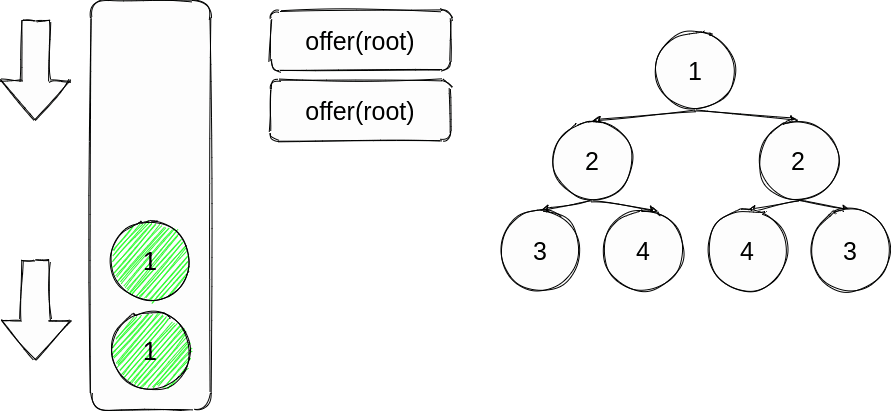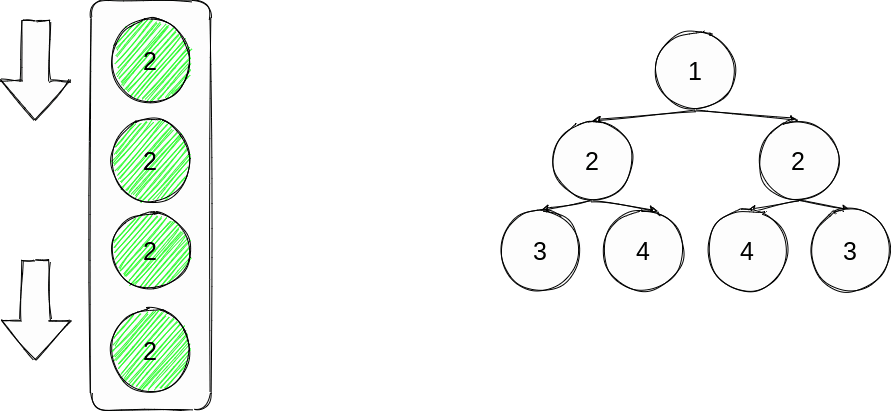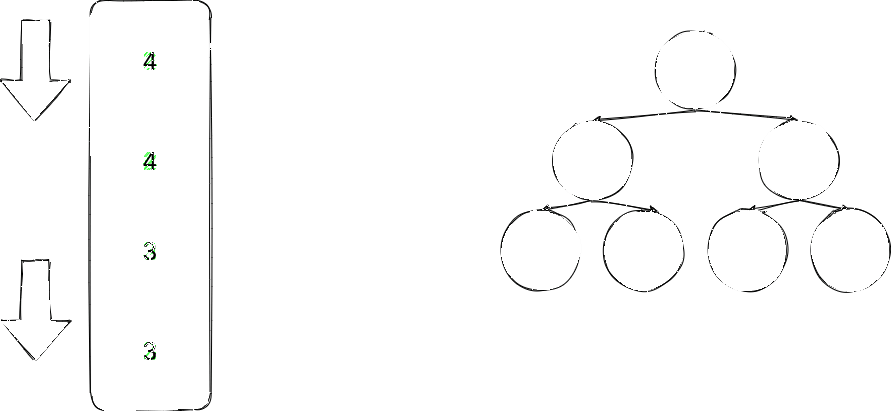
方法二：迭代

递归思路写完了，栈换成队列使用广度的方式完成同样的思路，还是再画个图

通过队列依次按照顺序比较offer进队列时就是一个树的左（右）与另一个树的右（左），poll出队列的两个也就是对应的，直到对队列没有后续进来的为空了仍然没出现不满足情况的，则是对称二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public boolean isSymmetric(TreeNode root) {
    return check(root, root);
}

public boolean check(TreeNode p, TreeNode q) {
    Queue<TreeNode> queue = new LinkedList<TreeNode>();
    queue.offer(p);
    queue.offer(q);
    while (!queue.isEmpty()) {
        //每次出两个
        p = queue.poll();
        q = queue.poll();
        //按照条件
        if (p == null && q == null) continue;
        if ((p == null || q == null) || (p.val != q.val)) return false;
        //按顺序进队列
        queue.offer(p.left);
        queue.offer(q.right);

        queue.offer(p.right);
        queue.offer(q.left);
    }
    return true;
}

时间复杂度与空间复杂度同上

总结

无外乎深度优先与广度优先，上面的两种解都是优的解在一次树的遍历过程中完成对是否是对称的判断。如果直接暴力的还可先遍历一遍得到序列或者数组再判断，比如先序遍历与后序遍历序列相反，比如中序遍历结果是回文的，总之我们要先对遍历熟悉。