题目信息

题目地址：https://leetcode-cn.com/problems/convert-sorted-array-to-binary-search-tree/

将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

示例:

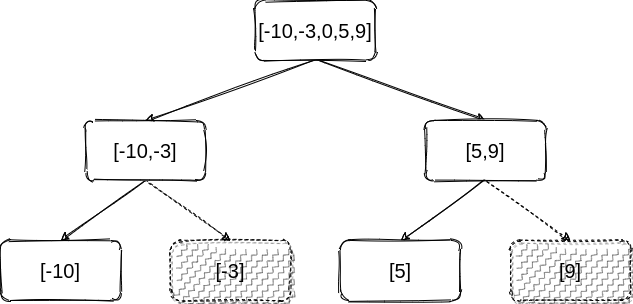
给定有序数组: [-10,-3,0,5,9],

一个可能的答案是：[0,-3,9,-10,null,5]，它可以表示下面这个高度平衡二叉搜索树：

1
2
3
4
5
     0
    / \
  -3   9
  /   /
-10  5

题解：递归（中序）

一个升序数组，转二叉树还是并且是搜索树（右子树小左子树），因此这个数组相当于是搜索树的中序遍历

对于示例的数组：[-10,-3,0,5,9]，转化为二叉搜索树结果是有很多

比如：

1
2
3
4
5
     0
    / \
  -3   5
  /     \
-10      9 
1
2
3
4
5
     5
    / \
  -3   9
  / \    
-10  0

题目当前是要得高度平衡的一个解（因此上面一个解是不满足的平衡的），因此尽量取中间作为根，就是最平衡的。

如果是偶数，取中间的两个任意的。如下要么-10为当前根-3为它的右子节点，要么-3为当前根-10为它的左子节点

因此我们可以推出递归

1
2
3
4
5
6
7
8
9
10
11
12
public TreeNode sortedArrayToBST(int[] nums) {
    return recurrence(nums, 0, nums.length - 1);
}
public TreeNode recurrence(int[] nums, int left, int right) {
    if (left > right) return null;
    // 除法运算向下取整，所以偶数取左边
    int mid = (left + right) / 2;
    TreeNode root = new TreeNode(nums[mid]);
    root.left = recurrence(nums, left, mid - 1);
    root.right = recurrence(nums, mid + 1, right);
    return root;
}

时间复杂度当然是O（n），平衡的缘故栈的深度为log2n因此空间复杂度为O（logn）

总结

总体来说还是比较好想的一个二分的这样一个东西，题目是求出满足条件的一解

1
int mid = (left + right) / 2;

这样取就得到的就是遇偶数取左边的解，如果加个1之后再除2就是取右了，或者加个随机数（0/1）。这样可以每次执行得到满足条件的树可能都不一样。

最后初级合集关于树这一章也结束了也是这个合集整个数据结构的篇章结束了，从开始对树这样的结构很生疏仅仅遍历操作就与线性数据结构有很大差别，到现在虽然短短5题已经对这样一个数据结构更熟悉了。从下个章节开始的就是关于算法思维向的篇章（排序、动态规划、数学等等）