题目信息

题目地址：https://leetcode-cn.com/problems/number-of-1-bits/

编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 ‘1’ 的个数（也被称为汉明重量）。

提示：

  • 请注意，在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，并且不应影响您的实现，因为无论整数是有符号的还是无符号的，其内部的二进制表示形式都是相同的。
  • 在 Java 中，编译器使用二进制补码记法来表示有符号整数。因此，在上面的 示例 3 中，输入表示有符号整数 -3。

示例 1：

1
2
3
输入：00000000000000000000000000001011
输出：3
解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 '1'。

示例 2：

1
2
3
输入：00000000000000000000000010000000
输出：1
解释：输入的二进制串 00000000000000000000000010000000 中，共有一位为 '1'。

示例 3：

1
2
3
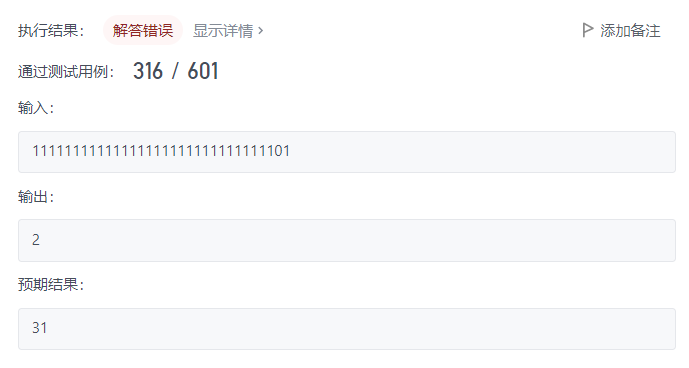
输入：11111111111111111111111111111101
输出：31
解释：输入的二进制串 11111111111111111111111111111101 中，共有 31 位为 '1'。

提示：

  • 输入必须是长度为 32 的 二进制串 。

进阶：

  • 如果多次调用这个函数，你将如何优化你的算法？

题解一：辗转相除

首先理清主逻辑，判断一组个其中有多少个1，对二进制来说每个位只有0或者1，对我们熟悉的十进制来说有0，1，2 ~，9。如果是十进制怎么判断这个位是非0呢，立马就知道是除以10

1
2
3
4
5
6
7
8
110 (十进制)
先判断个位是0还是非0
110除以10 可整除说明个位是0，留下11

进一步判断11
11除以10 不能整除说明非0的个数数加一 留下1

...

也就是说我们一步一步去判断每个位是否是0即可，对二进制来说非0也就是1，那么1的计数加一。

1
2
3
4
5
6
7
8
9
10
11
12
public int hammingWeight(int n) {
    // 计数1的个数
    int num = 0;
    while(n ！= 0){
        // 取余非0则余1，当前位是1
        if(n%2 != 0) num++;
        // 迭代n,直到n最后一个非0在个位则出循环
        n = n/2;
    }
    //记下最后一位非0数
    return ++num;
}

image-20210904165820519

那么这里有个问题就是对于负数是错误的，因为负数的二进制以补码呈现，像上述测试用例是-3，按照我们的上述逻辑应该是两个一和正3一样，就算加上最高位符号位的负号1也只能是三个一，但实际上负数以补码呈现的就像上述结果实际上是31个一。

因此上述解只是在数字层面的二进制是没问题的，在代码里面因为一些编译的问题就对负数就不行了

题解二：位运算

既然上述解是这样的问题，那我们就不去在数字层面弄，就按照它的规则去数一的个数，也不用转换什么的。其实是和解法一差不多的。因为把解法一翻译一下会变成如下：

1
2
3
4
5
6
7
8
public int hammingWeight(int n) {
    int num = 0;
    while(n = 0){
        if((n&1) != 0) num++;
        n = n>>1;
    }
    return ++num;
}

翻译就是把除运算换成位移运算，除以一个进制位就等于向右位移一次，对个位取余就等于与1进行与运算。这样逻辑上虽然和上面一样但是对于负数就不一样了

在代码中对于正数来说除以2和向右位移一位是一样的，负数就不一样了因为是一个补码串，你位移它就是用这个串去位移数的就是这个串，但你除以2得到的结果是和它的绝对值除2是一样的然后加个负号。如下：

1
2
3
4
5
6
7
8
3（8位）
0000 0011

-3
1111 1101

按除以2来，-3的结果也就是两个一
所以就用位运算，就不用管转换的问题了

但上面的代码是有问题的，上面的循环是为了循环到最高位的非0数，遍历完毕，这样不用遍历整个32位

对于负数来说就有问题，负数位移永远没有尽头，所以得改成for循环就循环这32位即可

1
2
3
4
5
6
7
8
public int hammingWeight(int n) {
    int num = 0;
    for(int i = 0; i < 32; i++){
        if((n&1) != 0) num++;
        n = n >> 1;
    }
    return num;
}

时间与空间复杂度都是O（1）

image-20210904230718590

题解三：位运算优化

前面题解一不用遍历完32为比如00010100 只用遍历到最高位的1即可也就是遍历5个。到了题解二位运算不能去判断是因为负数的二进制一直往右位移也永远不会等于0会进入无限循环。

所以只能找另外的方式怎么一步一步的计数1的出现然后在数字里面去掉或者变为0，直到最后一个1处理完，整个数就是0了就没必要继续遍历了。这个方法就是n & (n-1)，可以演示一下：

1
2
3
4
数字7也就是 0111
0111 & 0110 = 0110
0110 & 0101 = 0100
0100 & 0011 = 0000

也就是所每次都会去掉一个一，这个时候就可以计数一下。直到最终是0了，也就统计完最后一个1了。

1
2
3
4
5
6
7
8
public int hammingWeight(int n) {
    int num = 0;
    while(n != 0){
        n = n & (n-1);
        num++
    }
    return num;
}

image-20210904234047268

空间上去了一点可能是少了for循环的i

总结

这一题的话，主要是对于负数在Java里它的一个计算结果和常规是不一样的（这里不展开），因此就用位运算也就不存在转换。第二点就是对于一个int类型的整数它是32位，那么判断32位里有多少个1时，要不要遍历完32位才能出结果？这里就会有两个迭代方式一个是每次位移一个也就是丢掉最右边的数直到数字为0了后面也就不要遍历了，另一个是每次将最低位的1变为0，后者是更优的。因为001011对于第一种要遍历4次也就是每次丢一个直到最终数字为0，第二种方式只需要3次n & (n-1)能直接跳到最低位的1处理成0，中间的0都是直接跳过。n & (n-1)这个运算可以留意一下。还有一种最差的解法也就是转二进制串再数个数这样就没什么意义了相当与遍历了两次Integer.toBinaryString(n)。